许多考生在做题的过程中会遇到很多问题,多少会有一些知识点没有完全掌握,多做历年真题可以帮助同学们熟悉出题规律,总结命题重点,了解答题方向。接下来小编给大家整理了广东专插本数学历年真题供广大考生参考。
广东省2013年普通高等学校本科插班生招生考试
《高等数学》
一、单项选择题(本大题共5小题,每小题3分,共15分。每小题只有一个选项符合题目要求)
( )1.已经三个数列{an}、{bn}和{cn}满足an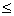 bn
bn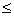 cn(n∈N+),且
cn(n∈N+),且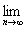 an=a,
an=a,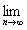 cn=c(a、b为常数,且a A.有界 B.无界 C.收敛 D.发散
cn=c(a、b为常数,且a A.有界 B.无界 C.收敛 D.发散
( )2.x=0是函数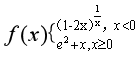 ,的
,的
A.连续点 B.可去间断点 C.跳跃间断点 D.第二类间断点
( )3.极限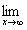 2xsin
2xsin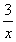 =
=
A.0 B.2 C.3 D.6
( )4.如果曲线y=ax-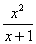 的水平渐近线存在,则常数a=
的水平渐近线存在,则常数a=
A.2 B.1C.0 D.-1
( )5.设f(x,y)为连续函数,将极坐标形式的二次积分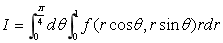 化为直角坐标形式,则I=
化为直角坐标形式,则I=
A.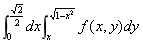
B.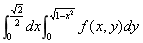
C.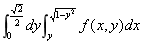
D.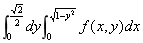
二、填空题(本大题共5小题,每小题3分,共15分)
6.设f(x)在点x0处可到,且f’(x0)=3,则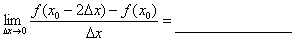
7.若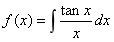 ,则f”(
,则f”(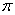 )=____ .
)=____ .
8.若曲线y=x3+ax2 +bx+1有拐点(-1,0),则常数b= ____.
9.广义积分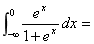 ________.
________.
10.设函数f(u)可微,且f’(o)=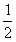 ,则z=f(4x2一y2)在点(1,2)处的全微分
,则z=f(4x2一y2)在点(1,2)处的全微分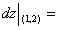 ______.
______.
三、计算题(本大题共8小题,每小题6分,共48分)
11.计算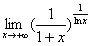 .
.
12.设函数y=f(x)由参数方程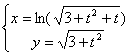 所确定,求
所确定,求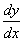
(结果要化为最简形式).
13.确定函数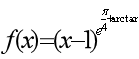 的单调区间和极值.
的单调区间和极值.
14.求不定积分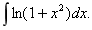 .
.
15.设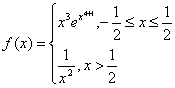 ,利用定积分的换元法求定积分
,利用定积分的换元法求定积分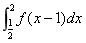 .
.
16.求微积分方程y’’一4y'+13y=0满足初始条件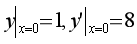 特解.
特解.
17.已知二元函数z=x(2y+1)x,求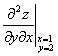 .
.
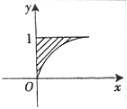
18.计算二重积分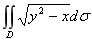 ,其中D是由曲线y=
,其中D是由曲线y=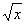 及直线y=1,x=0围成的闭区域.
及直线y=1,x=0围成的闭区域.
四、综合题(大题共2小题,第19小题12分,第20小题10分,共22分)
19.已知C经过点M(1,0),且曲线C上任意点P(x,y)(x≠0)处的切线斜率与直线OP(O为坐标原点)的斜率之差等于ax(常数a>0).
(1)求曲线C的方程;
(2)试确定a的值,使曲线C与直线y=ax围成的平面图形的面积等于 .
.
20.若当x→0,函数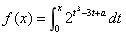 与x是等价无穷小量;
与x是等价无穷小量;
(1)求常数a的值;
(2)证明: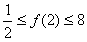 .
.
广东省2012年普通高等学校本科插班生招生考试
《高等数学》参考答案及评分标准
一、单项选择题(本大题共5小题,每小题3分,共15分)
1.A 2.C 3.D 4.B 5.C
二、填空题(本大题共5小题,每个空3分,共15分)
6.-6
7.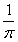
8.3
9.ln2
10.4dx - 2dy
三、计算题(本大题共8小题,每小题6分,共48分)
11.解:原式=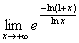 , (2分) .
, (2分) .
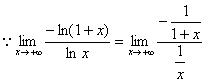 (4分)
(4分)
 (6分)
(6分)
12.解: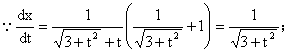
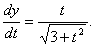 (3分)
(3分)
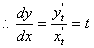 (结果没有化简扣2分). (6分)
(结果没有化简扣2分). (6分)
13.解:函数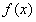 的定义域为
的定义域为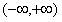 ,
,
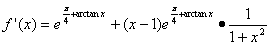
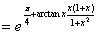 , (2分)
, (2分)
令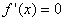 ,解得x=0,x=-1 因为在区间(-∞,-1)内,
,解得x=0,x=-1 因为在区间(-∞,-1)内,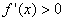 ;在区间(-l,0)内,
;在区间(-l,0)内,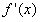 <0;
<0;
在区间(0,+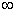 )内,
)内,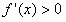 ,所以
,所以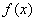
的递增区间是(-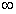 ,-1)及(0,+
,-1)及(0,+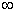 ),递减区间是(-1,0), (4分)
),递减区间是(-1,0), (4分)
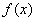 的极大值是
的极大值是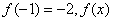 的极小值
的极小值 . (6分)
. (6分)
14.解: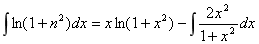 (2分),
(2分),
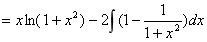
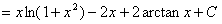 (6分)
(6分)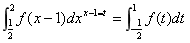 (2分)
(2分)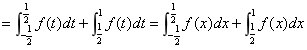
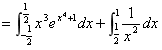 (4分)
(4分)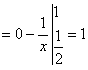 . (6分)
. (6分)16.解:由微分方程的特征方程r2 - 4r +13=0解得r=2±3i, (2分)
所以此微分方程的通解为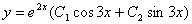 . (4分)
. (4分)
因为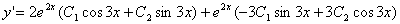 , 由
, 由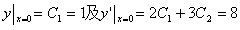
解得C1=1,C2=2,故所求特解为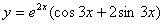 . (6分)
. (6分)
17.解: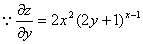 , (2分)
, (2分)
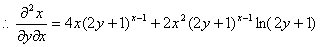 , (4分)
, (4分)
故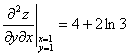 (6分)
(6分)
18.解:积分区域D如图:
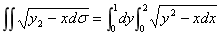 (3分)
(3分)
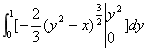
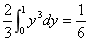
 (6分)
(6分)四、综合题(本大题共2小题,第19小题12分,第20小题10分,共22分)
19.解:(1)设曲线C的方程为y=厂O),由题意知
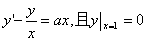 . (2分)
. (2分)
由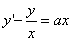 得
得
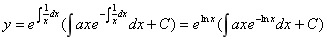 (4分)
(4分)
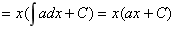 ,
,
因为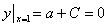 ,解得
,解得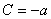
故曲线C的方程为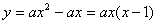 . (6分)
. (6分)
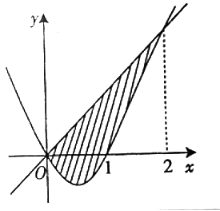
(2)如图,
由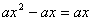 解得x=0,x=2, (10分)
解得x=0,x=2, (10分)
即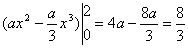 ,解得a=2. (12分)
,解得a=2. (12分)
由题意知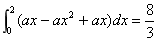 ,
,
20.解:(1)解:由题意知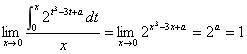 , (4分)
, (4分)
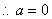 .
. (2)证: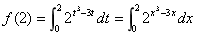 ,
,
设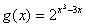 ,
,
则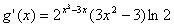 , (6分)
, (6分)
令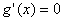 ,在区间(0,2)内解得x=l,
,在区间(0,2)内解得x=l,
因为g(0)=1,g(1)=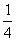 ,g(2)=4,
,g(2)=4,
所以g(x)在区间[0,2]上的最大值为4,最小值为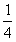 . (8分)
. (8分)
由定积分的估值定理可得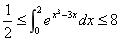 ,
,
所以有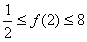 . (10分)
. (10分)
华师南粤优师专插本辅导中心开设暑假班、寒假班、周末班、全科班等教学班型,为广大专插本考生提供专插本视频课程,专插本辅导教材,在线题库等,助力学生实现专插本梦想。

想要报名专插本的学生,欢迎在线咨询招生老师哦!我们已经帮助了大量的专科学子顺利插入本科院校就读,真正获得了全日制本科学历!从此,启肮美好的人生!
华师南粤优师专插本
培训路线指引图
地址:华南师范大学(石牌校区) 产业大楼113办公室 (华师地铁口E出口)